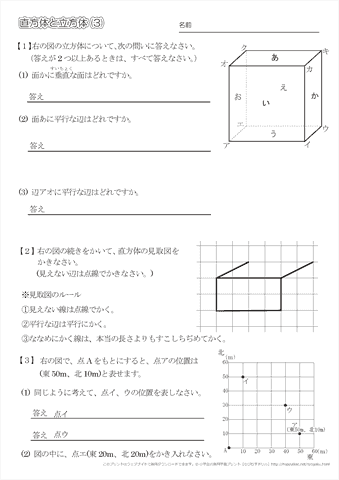
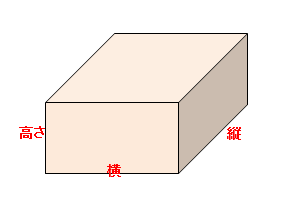
(4)次に(3)の立方体が 段積めるので,右上 の直方体の体積は(1)の大きさの立方体が × 個分あるから, cm³ となります。 2 直方体や立方体の体積 学 年 組 氏 名 6cm 6cm 6cm 12m 25m 2m 直方体の体積=たて×横×高さ 4cm 3cm 5cm × × × 2cm 45cm 3cm 3cm直方体や立方体の体積 井土ヶ谷小学校 5年生課題 スマートフォンの場合は, たて向きにしましょう。 パソコンの場合は, 右のように画面を合わせましょう。 タブレット端末の場合は, たて向きにして 1画面ずつみるように注意しましょう。 スタートあ い う え お か き 名 前 4年 組 う, お え あ, き 直方体 直方体 8 12 6 0 直方体 8 12 4 2 立方体 8 12 0 6 立方体 平面 (教科書13〜22ページ) ① 面 めん あから面 めん
直方体と立方体
直方体 と 立方体 問題 集
直方体 と 立方体 問題 集-直方体の大きさは,たて,横,高さの3つの辺の長さで決まるんじゃ! 立方体の大きさは,たて,横,高さが同じなので,1辺の長さで決まるんじゃ! 直方体や立方体は,まわりが平らな面だけでできています。 平らな面のことを平面 へいめん というんじゃ!こまれている形を、( 直方体 )といいます。 (3) 正方形だけでかこまれている形を、( 立方体 )といいます。 (4) 直方体や立方体で、長方形や( 正方形 )の形をしたところを ( 面 )といいます。



4年の 直方体と立方体 のソフト 平行な辺 横山験也のちょっと一休み
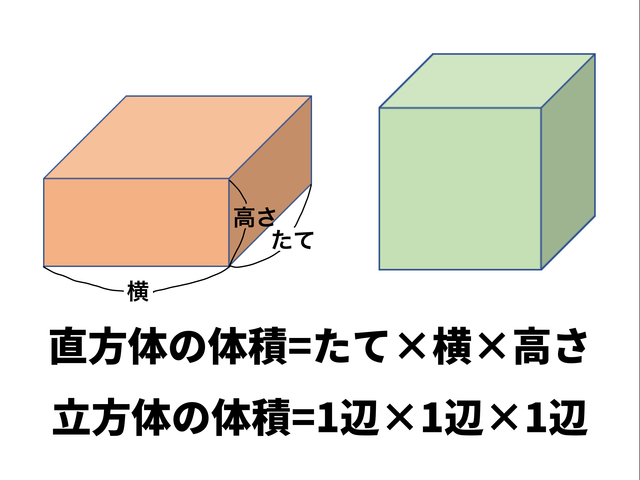
直方体や立方体などの全体の形がわかるようにかいた図を見取図 みとりず といいます。 学習日 年 月 日 単 元 年 組 番 4年「直方体と立方体」 氏名 長方形か正方形 をかく。 てん開図 図のように、となり あった面をかく。 見えない辺は点線 でかく。概要 (表示しない) 基本的な立体図形についての理解を深め、空間概念の基礎を養うために、見取図をかく授業展開を考えました。 図形の構成要素や位置関係に着目し、図形についての見方を豊かにしていくために、立体をじっくり観察できるように立方体の体積の求め方 = 一辺 × 一辺 × 一辺 直方体の体積の求め方 = たて × 横 × 高さ
立方体 ・ 長方形だけか,長方形と正方形 で囲まれた箱の形を 直方体 といいます。 ・ 同じ大きさの6つの正方形 で囲まれた箱の形を 立方体 といいます。の直方体の体積は(1)の大きさの立方体が 個分あるから, cm³ となります。 2 直方体や立方体の体積 学 年 組 氏 名 6cm 6cm 6cm 12m 25m 2m 直方体の体積=たて×横×高さ 4cm 3cm 5cm 2cm 45cm 3cm 3cm 216cm3 27cm3 m3 1辺が1mの立方体 1c3) 4 5 たて 横(50)直方体と立方体 日 付 1 立方体と直方体 (1) 下の図のように、長方形や 長方 形と正方形で囲まれた立体を、何と いうでしょう。 (2) 下の図のように、正方形で囲まれ た立体を、何というでしょう。 2 立方体と直方体の面、辺、頂点
直方体の体積 ケーキ作り。 材料の分量を計算するため (レシピに載っている型と手持ちの型が違うので) 加工金属の質量を求めるのに自分の計算の答え合わせとして活用させていただきました。 リュックの容量比較で参考にさせていただきました。立方体 12 6 8 直方体 12 6 8 解説立方体と直方体の見取図をかいて,確かめましょう。 2 図のような展開図を組み立てたときにできる, てんかいず 直方体について,次の問いに答えましょう。 (1)面②に平行な面はどれですか。 答え 面④ (2)面①に76 77 第19回 立方体と直方体の性質 応用問題 A 下の図のように,3つの面に,1から3までの数字がかかれた立方体の展開図 が2つあります。これらの展開図は,組み立てると全く同じ立方体になります。
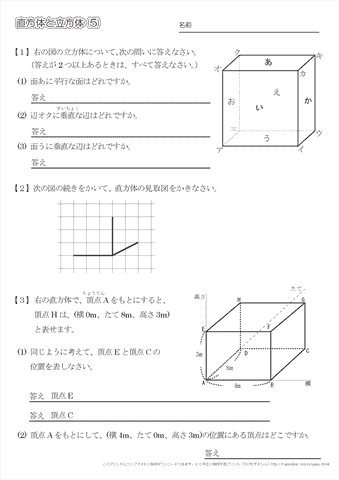



小学4年生の算数 直方体と立方体 問題プリント ちびむすドリル 小学生




โน ตของ 直方体と立方体の体積 ช น Primary算数 Clear
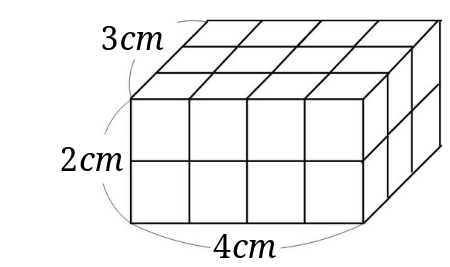
柱体を構成する要素に着⽬ 柱体の⾯の位置関係に着⽬ ⾯の形に着⽬すると、三角柱・四角柱 五角柱・・・に分類できるね。 底⾯と側⾯に着⽬すると、直方体や立 方体は四⾓柱、さらに⾓柱ともみるこ とができるよ。 直方体と同じように、底⾯どうしが直方体や立方体の体積を、計算で求める方法を考えよう。 まず、㋒の直方体は、1cm³の立方体の何こ分か計算で求めてみましょう。 1cm³の立方体が何こあるのかを求めるには?? ・面積のときは計算で求められたなぁ。今日も、直方体,立方体の体積について学習をしていきます。 めあてを読んで、ワークシートに書きましょう。 めあて 直方体と立方体の体積を、計算で求める方法を考えよう。 (3)㋒の直方体の体積の求め方について考えていきます。



兵庫県実践事例 算数小学校6年




Qb説明 4年 直方体と立方体 On The App Store
直方体や立方体のかさの表し方を考えよう ㋒の直方体と㋓の立方体の体積を求めましょう。 ㋒の立方体は、1㎤の立方体の何個分か調べましょう。 (1)1だんめには、1㎤の立方体が何こならびますか。 (2)何だん積めますか。直方体,立方体の体 積を求める公式を理 解し,公式を適用し て体積を求めること ができる。 縦4cm,横6cm,高さ5cmの直方体と1辺4cmの立方体の体積を計算で求める方法を考える。 それぞれ1cm3の立方体の何こ分か調べる。直方体や立方体の形を切り開いてかいた図を展開図という。 立方体の展開図を考えてみましょう。 上の図のほかに,次のような展開図もあります。 次のア~エのうち,立方体の展開図になっているものをすべて選 えら び,ア~エ の記号で答えなさい。




ひごと粘土玉ではこの形を学習 家庭学習レシピ



直方体と立方体
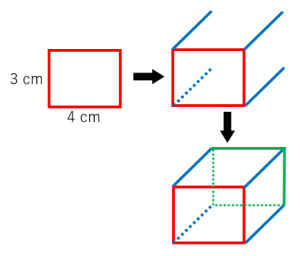
体 と 立 方 体 の 体 積 2 どちらがどれだけ大きいかを考える。(直方体と立方体を比べる) 体積の意味、体積の単位「cm 3 」を知る。 ・体積も単位となる体積をもとに数値化できることを考える。 ・体積の意味と単位「cm 3 」を理解する。 3直方体とは、立方体とは 直方体とは、箱の形でたて・よこ・高さの数字が3種類または2種類のものです。面の形は、長方形だけの場合と長方形と正方形がある場合があります。 立方体とは、箱の形でどの辺も同じ長さで面の形がすべて正方形のものです。 練習問題 下の形を直方体と立方体に分けましょう。 直方体・・・( )つづいて、立方体・直方体がこれらの公式で求められる理由について説明していきます。 立方体・直方体の体積が公式で求められる理由 今回2つの説明の仕方を紹介します。 説明1「長方形を積み上げる」というイメージ
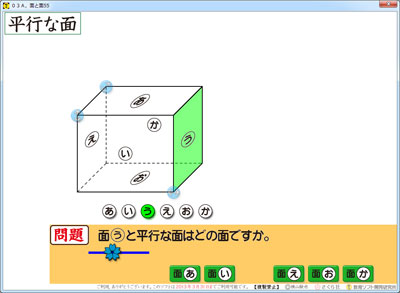



4年の 直方体と立方体 のソフト 平行な面 さくら社




Qb説明 4年 直方体と立方体 App Download Android Apk
第4学年 算数科「直方体と立方体」評価規準 身のまわりの立体には,基本的な立体に似た形があることに気づき,調べることを通して,直方体や立方体の意味を理解する。 ①~⑤の立体からあ,い,うの形と似ているものを見つける。 B:概ね似ている構成要素に着目して直方体、立方体の特徴、性質を理解する。 小学生・中学生が勉強するならスクールTV。 全国の学校の教科書に対応した動画で学習できます。立方体は立方体の特殊なケースです。 立方体は、同じサイズの正方形の面が90度の角度で交わる6面の3次元図形であるのに対して、直方体は、すべてが90度で交わる6つの面で構成される箱型のオブジェクトです。 角度。 立方体の形状は、すべての辺が同じ




Pin On Matematicas




世界一分かりやすい算数 小4 直方体と立方体
第19回(放送日:3月7日、3月14日) 博士の居場所を推理せよ ~立方体~ 博士が行方不明との一報が入る。 手がかりは、博士が残した菓子箱の展開図。 箱を建物に見立てて、居場所を知らせようとしていたのだ。 ゼロは箱を組み立て場所を突き止める!直方体や立方体の体積を計算で求めるには、次のようにします。 ①たて、横、高さをはかる。 ②3つの辺の長さを表す数をかける。 まとめ 直方体や立方体の体積は、次の公式で求 めることができる。 直方体の体積=たて×横×高さ 立方体の体積=1辺×1辺×1辺直方体と立方体の体積① <学習した日 月 日> 考えよう あと いの展開図を組み立てると、右のような立体になります。どちらがどれだけ大きいで しょうか。 たて、横、高さの辺の長さをそれぞれ合わせると、



直方体と立方体を描く Ipadとiphoneで教師の仕事をつくる




動画で学習 1 直方体と立方体 算数
直方体の大きさは、 、 、 の3つの辺の長さで 決まります。 立方体の大きさは、 の長さで決まります。 直方体や立方体などを にそって切り開いて、 の上に広げた図を と 言います。 5 4で切り開いた形を紙に写しとってみましょう。( 直方体と立方体 )の学習をふりかえって 1 次の にあてはまることばや数をかきましょう。 ① 長方形や,長方形と正方形でかこまれた形を といいます。 ② 正方形だけでかこまれた形を といいま す。 ③ 直 ちょく 方 ほう 体 たい や立 りっ 方 ぽう 体直方体と立方体 ICT教材eboard(イーボード) 教材を見てみる 使い方ガイド ログイン 教育現場でのご活用 算数にもどる
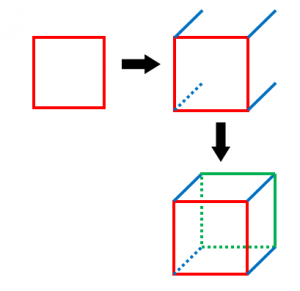



立方体と直方体の見取り図の書き方 具体例で学ぶ数学



直方体と立方体
直方体と立方体 (1) 直方体と立方体 の中にあてはまる言葉をかきましょう。 あのように,長方形だけでかこまれた形や,長方形と正方形でかこまれた形を といいます。 いのように,正方形だけでかこまれた形を といいます。 上の立体の頂点,辺,面について考えましょう。③ 直方体や立方体の体 たいせき 積は,次の公式で求 もと められます。 直方体の体 たいせき 積= × × 立方体の体 たいせき 積= 1 いっぺん 辺 × × ④ 右の直方体の体 たいせき 積を求 もと めましょう。年 組 番 名前 4155 直方体と立方体 展開図 ③ 1 下の図で、直方体の正しい展開図はどれですか。 2 右の直方体の展開図を組み立てます。 ①点サと重なる点はどれですか。 ②点キと重なる点はどれです



4年算数 直方体と立方体 1 わかる教え方のポイント




小学5年生の算数 動画 直方体と立方体の体積 の問題 19ch
〇直方体,立方体,円柱,球などの立体図形の 基礎的概念 〇形や機能に着目した,立体図形の分類 〇立体図形を構成している平面図形の特徴 第2学年『はこの形』 〇直方体,立方体の意味 〇直方体,立方体の面,辺,頂点の考察



小学4年生の算数 直方体と立方体 問題プリント ちびむすドリル 小学生
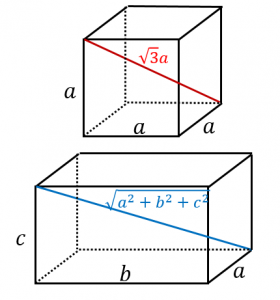



立方体と直方体の対角線の長さ 具体例で学ぶ数学




世界一分かりやすい算数 小4 直方体と立方体



1




世界一分かりやすい算数 小4 直方体と立方体




時空先生のドリルプリント 直方体と立方体の辺の数 頂点の数 面の数 算数ドリル 算数プリント 図形の問題 家庭学習 復習 先取り学習 基礎の定着 時空先生 Facebook




4年 算数 直方体と立方体 ゲーム 教育なんでも館



4年の 直方体と立方体 のソフト 平行な辺 横山験也のちょっと一休み



Http Www Nikkyoken Com Ikousochi Pdf H21 Sansu5d Pdf
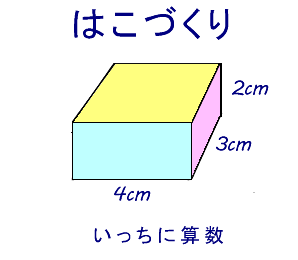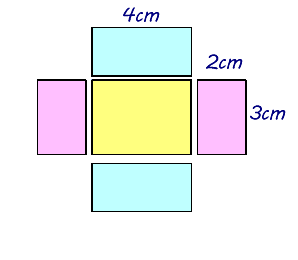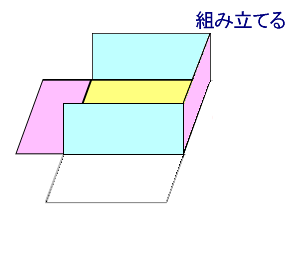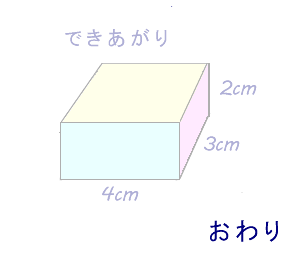



4年算数 直方体と立方体 2 わかる教え方のポイント
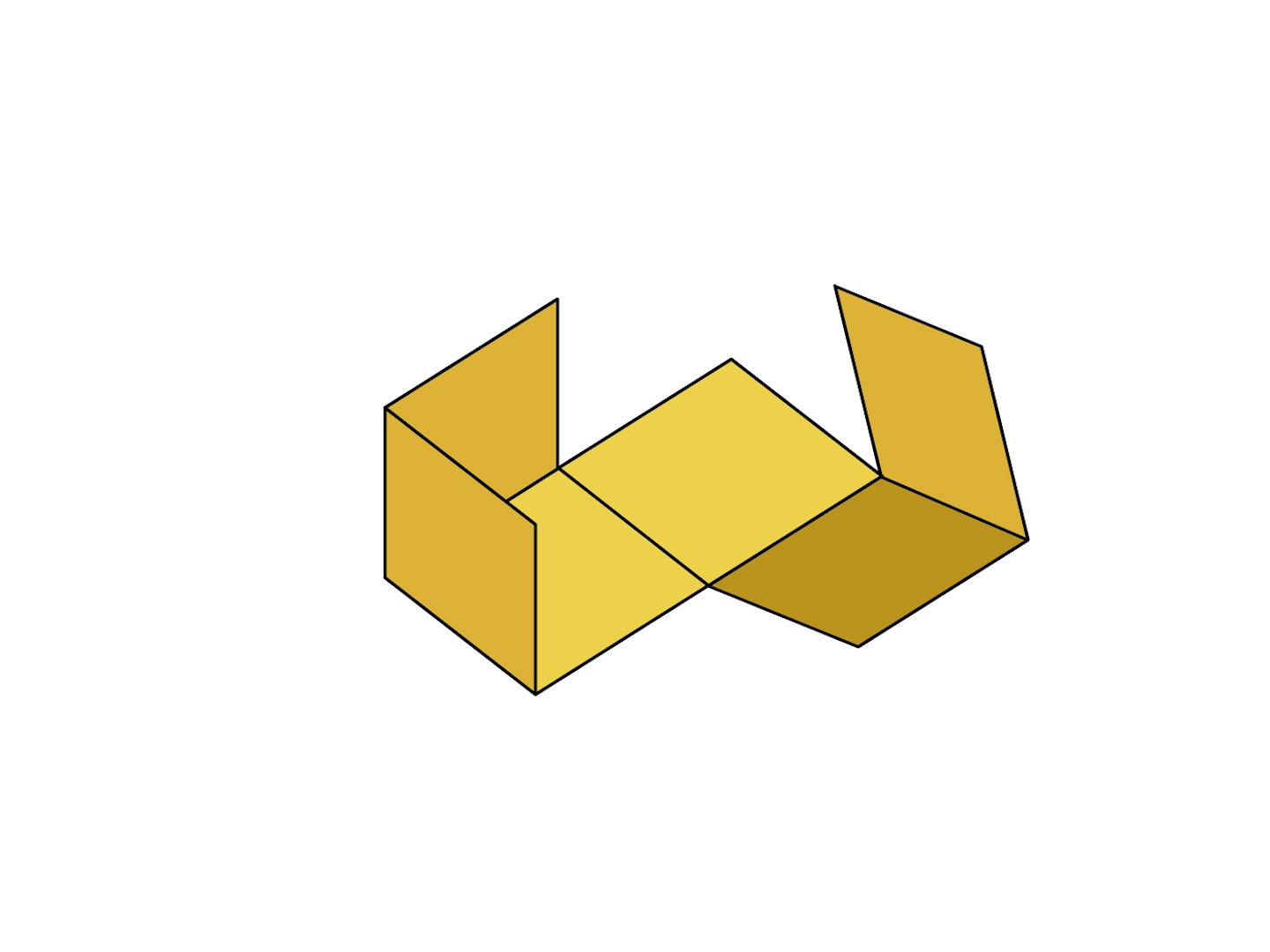



4年 展開図ってなんだろう 算数イメージ動画集 大日本図書




展開図と見取り図の問題プリント 直方体と立方体 無料の算数プリント



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式
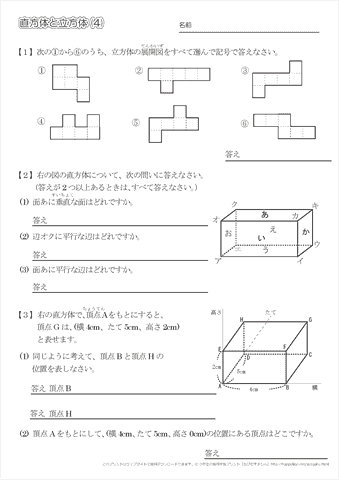



小学4年生の算数 直方体と立方体 問題プリント ちびむすドリル 小学生



4年算数 直方体と立方体 1 わかる教え方のポイント




直方体と立方体 Flashcards Quizlet



直方体と立方体



直方体の計算 もう一度やり直しの算数 数学
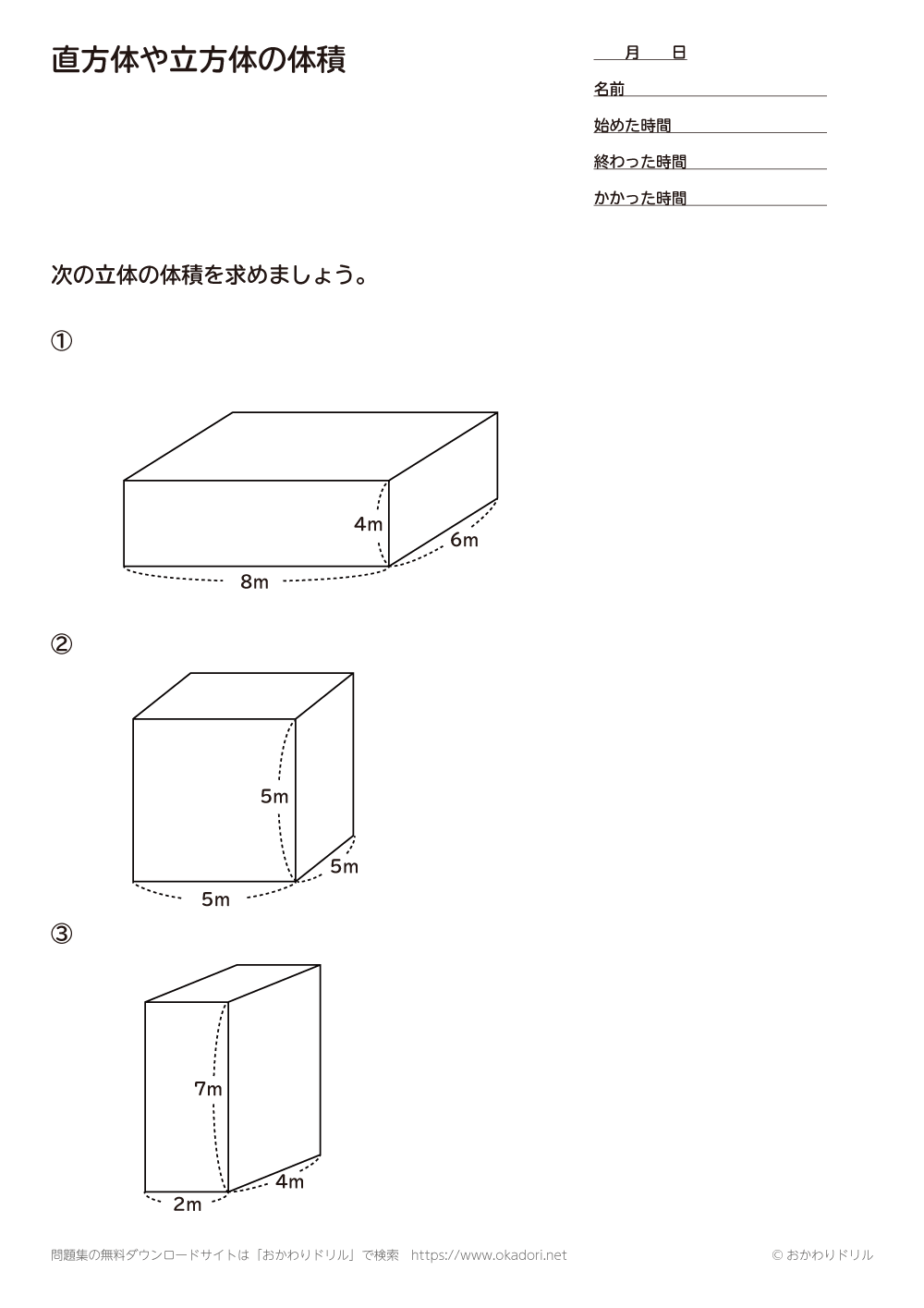



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル



パワーポイント教材 那須烏山市立烏山小学校



数学のことなんですが 立方体と直方体と四角柱は何が違うのでしょうか Yahoo 知恵袋
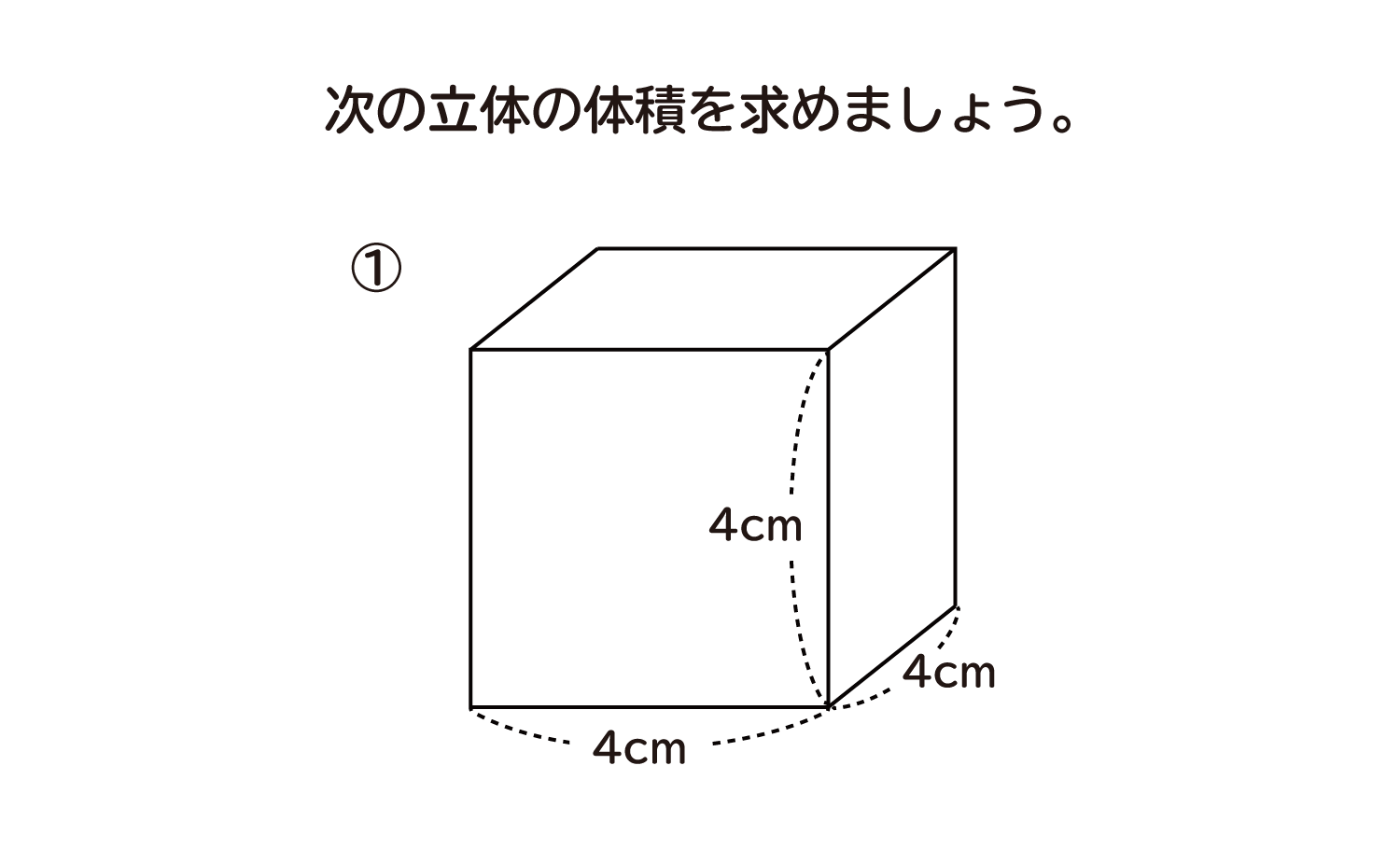



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル




ウチダ 教材総合カタログ 小学校
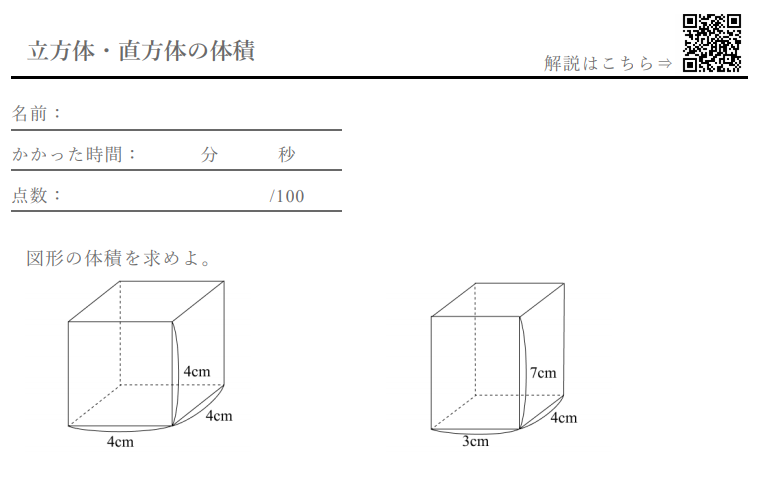



立方体 直方体 の体積 計算ドリル 問題集 数学fun
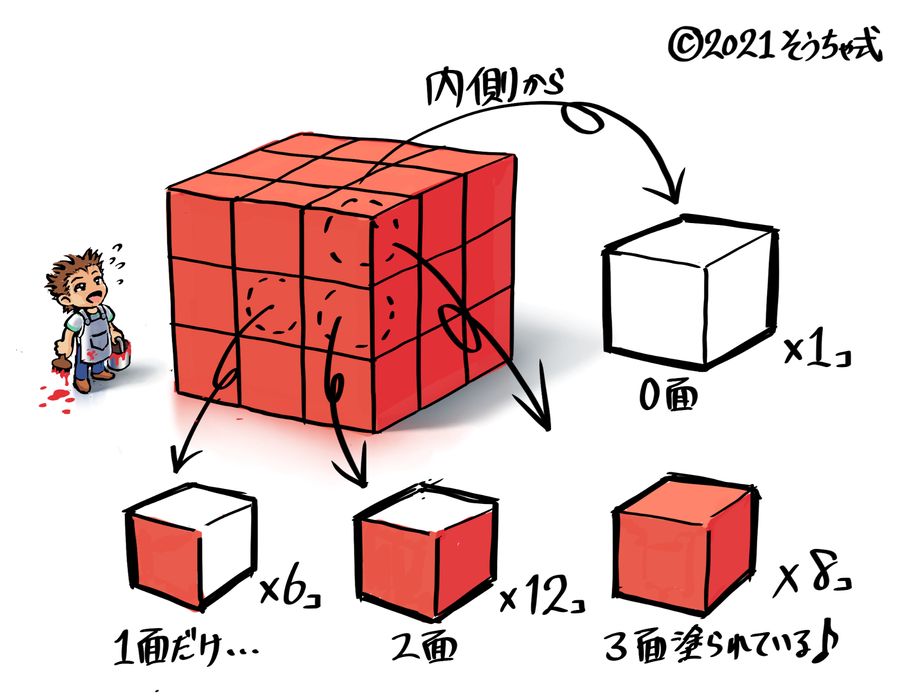



中学受験 直方体 立方体のまとめ 立体図形 そうちゃ式 受験算数 2号館 図形 速さ



1



Www Town Sugito Lg Jp Doc Lib 2 E7 9b B4 E6 96 B9 E4 93 81 A8 E7 Ab 8b E6 96 B9 E4 93 E7 Ac Ac E4 B8 E5 B0 8f E4 90 E8 97 E7 Ab B9 E5 B1 B1 Pdf
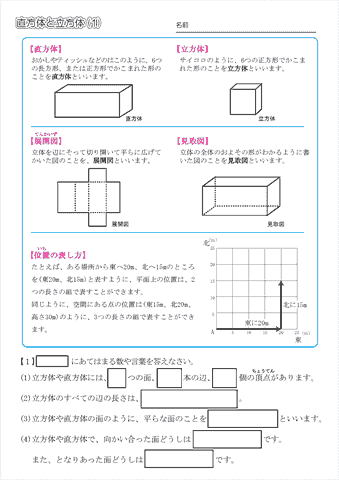



小学4年生の算数 直方体と立方体 問題プリント ちびむすドリル 小学生



Ipad用学習支援ツール qb説明 算数 4年 直方体と立方体 スズキ教育ソフト




直方体と立方体 Ict教材eboard イーボード




直方体と立方体 Ict教材eboard イーボード
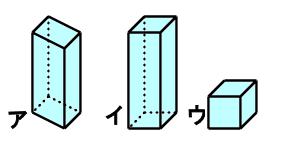



直方体と立方体



直方体や立方体の体積を求める公式は どうして たて 横 高さ なの みけねこ小学校



1




Amazon 算数教材 立体図形 直方体 立方体 3d幾何学図形模型 知育玩具 数学学習玩具 算数教材として活用可能 学用品 文房具 オフィス用品



Http Nk Minamidai E La Coocan Jp Kadai 5nen R0518 5nen Math02 2 6 Pdf



直方体と立方体 箱の形を調べよう 久木田雅義先生 算数4年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



Www Shinko Keirin Co Jp Keirinkan Sho Sansu Support Keyseat Data Sansu 4nen3 03 Pdf




小学4年生算数 直方体と立方体 面 辺の垂直 平行を理解する 無料プリントあり 子供と一緒に家庭学習



数学の空間図形で必要な直方体や立方体等の図形の描き方は 立体を簡単に描くコツとは さびねこ中学校



Www Shinjuku Ed Jp Es Ochiai6 Spn 8615 Pdf



立方体と直方体 On Vimeo



Http Www City Kofu Yamanashi Jp Gakkoukyoiku Gakusui H21 Print Sp 6 6 1 Pdf



立方体と直方体の見取り図の書き方 具体例で学ぶ数学




小学5年生の算数 動画 直方体と立方体の体積 の問題 19ch




小学校5年 算数 直方体や立方体のかさの表し方を考えよう シンキングツール 思考ツール 授業案
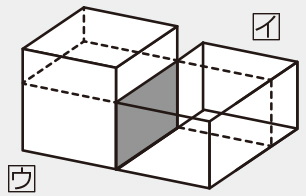



小5算数 直方体と立方体の体積 指導アイデア みんなの教育技術




立方体と直方体の面 辺 頂点 Youtube




小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすマンスリー 学習ポスター テストクイズ 3ステップ学習 算数 表面積 小学校 算数




すきるまドリル 小学4年生 算数 直方体と立方体 無料学習プリント すきるまドリル 無料学習プリント




小5 算数 小5 3 直方体と立方体の体積 Youtube




直方体と立方体 Flashcards Quizlet
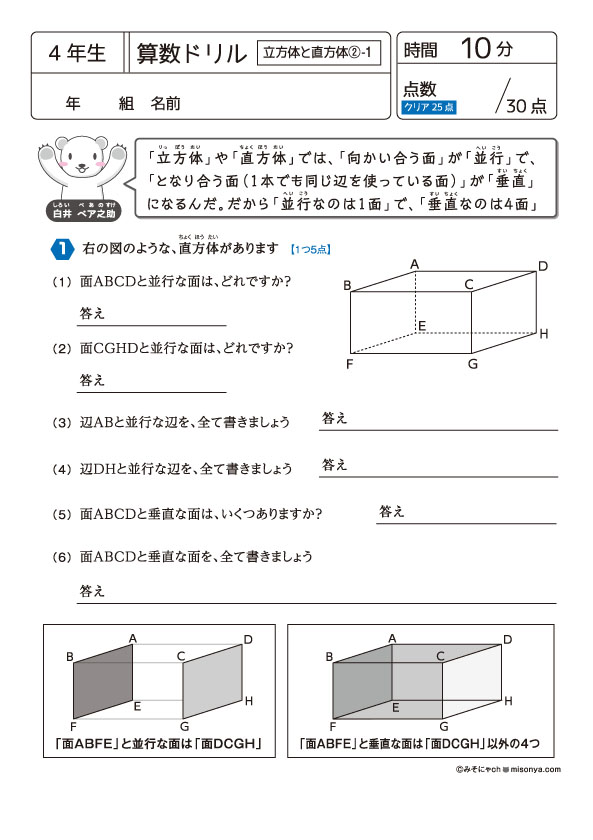



無料の学習プリント 小学4年生の算数ドリル 立方体と直方体2 みそにゃch




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館



4年 直方体と立方体 のわかりやすいソフト 横山験也のちょっと一休み
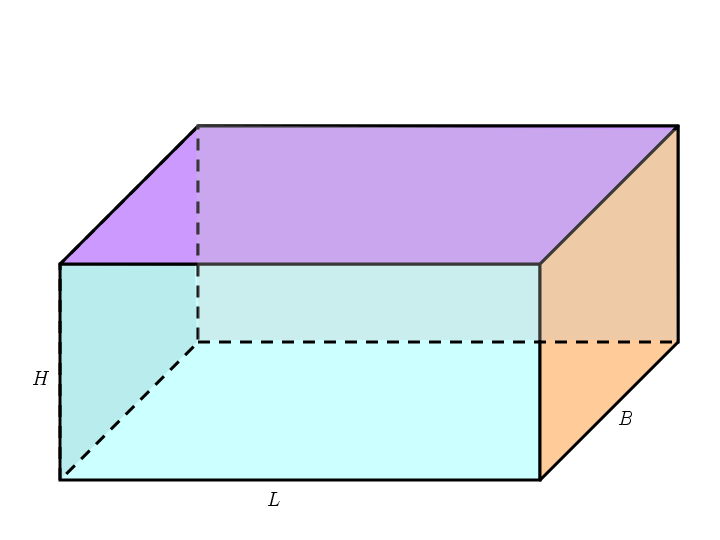



直方体 Wikipedia




小4算数 直方体と立方体 指導アイデア みんなの教育技術



4年 算数 直方体と立方体 大井小学校公式ホームページ
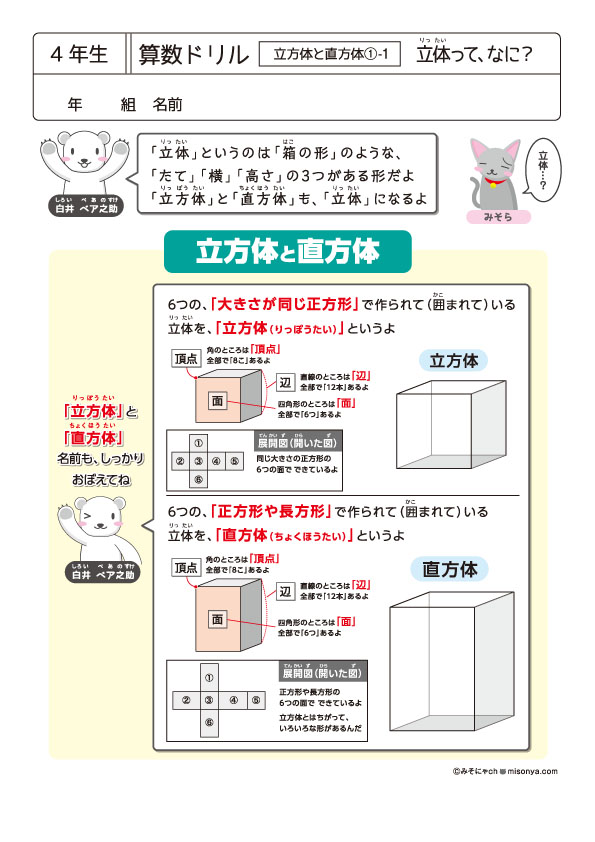



無料の学習プリント 小学4年生の算数ドリル 立方体と直方体1 みそにゃch




直方体 立方体の体積 Youtube
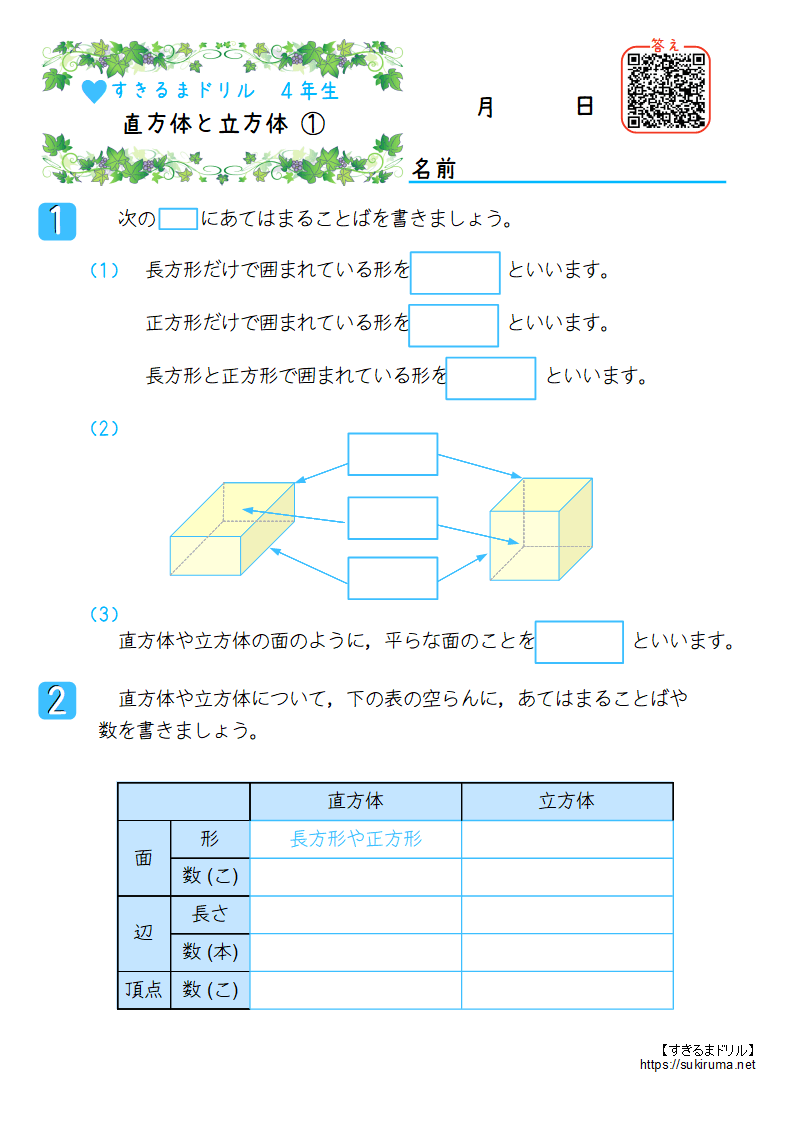



すきるまドリル 小学4年生 算数 直方体と立方体 無料学習プリント すきるまドリル 無料学習プリント




楽天市場 算数 立方体 直方体の通販




心に強く訴える 立方体 と 直方体




世界一分かりやすい算数 小4 直方体と立方体
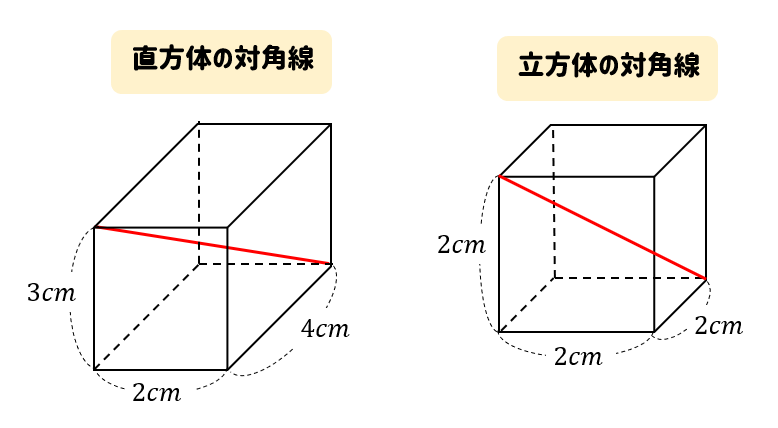



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ




直方体と立方体の体積 算数 数学が好きになりmath




直方体と立方体 算数 学習 Yahoo きっず



直方体と立方体




直方体と立方体の導入 条件規制の手法で 八戸市立市野沢小学校
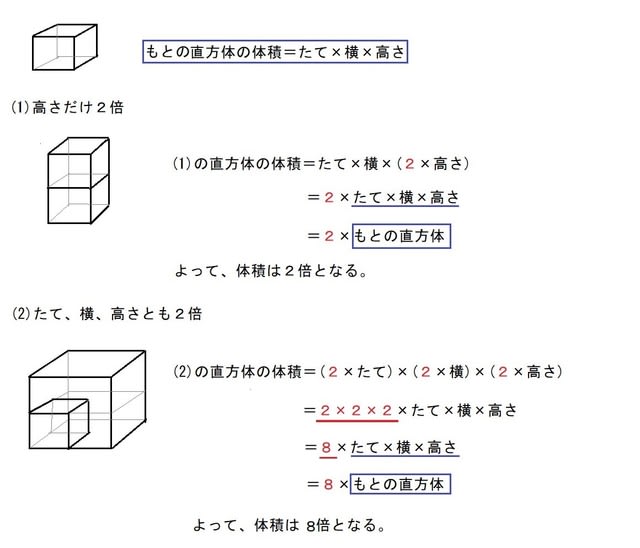



直方体 立方体の体積 小5 きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support



直方体の展開図 54通り を整理 算数の広場




いっちに算数サイトの人気記事 4年 直方体と立方体 いっちに算数 のブログ




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 学習 数学ノート



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー




直方体と立方体の対角線 無料で使える中学学習プリント
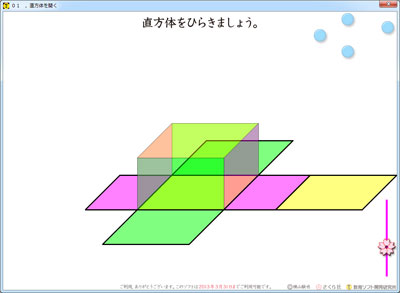



4年の 直方体と立方体 直方体を開くソフト さくら社




Amazon 8個 プラスチック おもちゃ 立方体 円錐 直方体 図形モデル 数学学習 すうじ 図形 計算 おもちゃ




4年 算数 直方体と立方体




授業 直方体と立方体 1 算数 小4 群馬県 Youtube



3



直方体と立方体 教育考現学




小学4年生算数 直方体と立方体 面 辺の垂直 平行を理解する 無料プリントあり 子供と一緒に家庭学習



ドリルズ 小学4年生 算数 の無料学習プリント算数 直方体 立方体



4年算数 直方体と立方体 1 わかる教え方のポイント




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




5年 算数 直方体と立方体 複合図形 授業デザイン研究所




直方体と立方体 Ict教材eboard イーボード



0 件のコメント:
コメントを投稿